
(Nickelback approves of Graph Deep Learning 😎)
Graph Deep Learning (GDL) is an up-and-coming area of study. It’s super useful when learning over and analysing graph data. Here, I’ll cover the basics of a simple Graph Neural Network (GNN) and the intuition behind its inner workings. Don’t worry, there are tons of colourful diagrams for you to visualise what’s happening!
❓ Graph, who?
A graph is a data structure comprising of nodes (vertices) and edges connected together to represent information with no definite beginning or end. All the nodes occupy an arbitrary position in space, usually clustered according to similar features when plotted in 2D (or even nD) space.

This is a graph: a bunch of interconnected nodes that represent entities.
The black arrows on the edges represent the kind of relationship between the nodes. It shows whether a relationship is mutual or one-sided. The two different kinds of graphs are directed (connection direction matters between nodes) and undirected (connection order doesn’t matter). Directed graphs can be unidirectional or bidirectional in nature.
A graph can represent many things — social media networks, molecules, etc. Nodes can be thought of as users/products/atoms while the edges represent connections (following/usually-purchased-with/bonds). A social media graph may look like this with nodes as users and edges as connections:
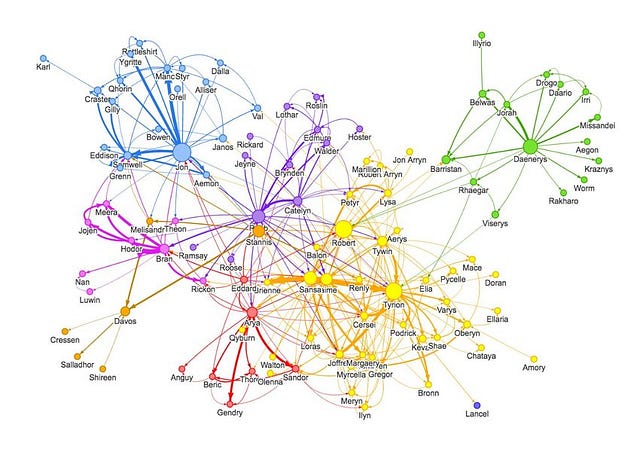
Nodes represent users while edges represent the connection/relationship between two entities. Social media graphs are usually a whole lot more enormous and complex!
📑 What you need to know
Here, I’ll be mentioning some concepts right off the bat. I’ll be talking about recurrent units, embedding vector representations, and feed-forward neural networks. It’s nice to know a fair bit of graph theory (as in, what a graph is and what it looks like) as well.
There may be terms you are familiar with. Fret not! For all the confusing jargon, I’ve linked the best explanation I can find covering the basics of the said concept. That way, you can read further into the concepts while also understanding the role they play in Graph Neural Networks.
🚪 Enter Graph Neural Networks
Each node has a set of features defining it. In the case of social network graphs, this could be age, gender, country of residence, political leaning, and so on. Each edge may connect nodes together that have similar features. It shows some kind of interaction or relationship between them.
Suppose we have an arbitrary graph G with the following vertices and edges:
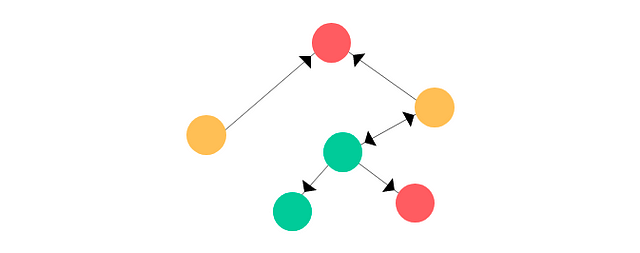
It’s the same graph from above.
For simplicity’s sake, let’s assume that the feature vector is a one-hot-encoding of the current node’s index. Likewise, the label (or class) could be the colour of the node (green, red, and yellow as shown above). It’d look something like this:
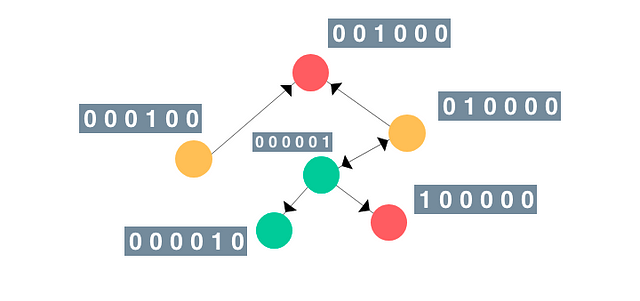
The order they are in doesn’t really matter.
Note: In reality, try not to use one-hot-encodings because the order of the nodes may be messy. Rather, use features that uniquely identify the node (e.g. age, gender, political leaning, etc. for Social Media or numerical chemical properties for molecular studies).
Now that we have our one-hot-encodings (or embeddings) of the nodes, let’s alter the graph by bringing in neural networks into the mix. All the nodes are converted into recurrent units (or any neural network architecture, actually; I’m using recurrent units here) and all the edges house simple feed-forward neural networks. It looks something like this:
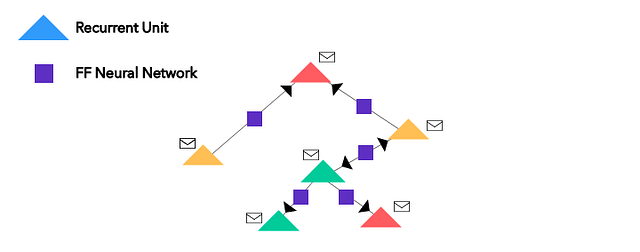
The envelopes are simply the one-hot-encoded (embedding) vectors for each node (recurrent unit, now).
📮 Message Passing
Once the conversion of nodes and edges are completed, the graph performs Message Passing between the nodes. This process is also called Neighbourhood Aggregation because it involves pushing messages (aka, the embeddings) from surrounding nodes around a given reference node, through the directed edges.
Note: Sometimes, you can use a different neural network for different types of edges; one for unidirectional and another for bidirectional. That way, you can still capture the spatial relationships between nodes.
In terms of GNNs, for a single reference node, the neighbouring nodes pass their messages (embeddings) through the edge neural networks into the recurrent unit on the reference node. The new embedding of the reference recurrent unit is updated by applying said recurrent function on the current embedding and a summation of the edge neural network outputs of the neighbouring node embeddings. Let’s zoom into the top red node and visualise the process:
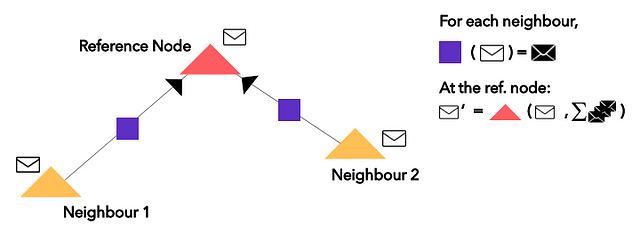
The violet square is a simple feed-forward NN applied on the embeddings (white envelopes) from the neighbouring nodes. The recurrent function (red triangle) applied to the current embedding (white envelope) and summation of edge neural network outputs (black envelopes) to obtain the new embedding (white envelope prime).
This process is performed, in parallel, on all nodes in the network as embeddings in layer L+1 depend on embeddings in layer L. Which is why, in practice, we don’t need to ‘move’ from one node to another to carry out Message Passing.
Note: The sum over the edge neural network outputs (black envelopes in the diagram) is invariant of the order of the outputs.
🤔 What do I do with the final vector representations?
Once you perform the Neighbourhood Aggregation/Message Passing procedure a few times, you obtain a completely new set of embeddings for each nodal recurrent unit.
Through the timesteps/rounds of Message Passing, the nodes know more about their own information (features) and that of neighbouring nodes. This creates an even more accurate representation of the entire graph.
For further processing in higher layers of a pipeline, or simply to represent the graph, you can take all the embeddings and sum them up together to get vector H that represents the whole graph.
Using H is better than using an adjacency matrix because these matrices don’t represent the features or unique aspects of the graph despite any graph contortion–simply the edge connections between nodes (which isn’t really important based on some contexts).
To summarise this step, we sum together the final vector representations of all nodal recurrent units (order-invariant, of course) use this resulting vector as inputs to other pipelines or to simply represent the graph. This step looks like this:
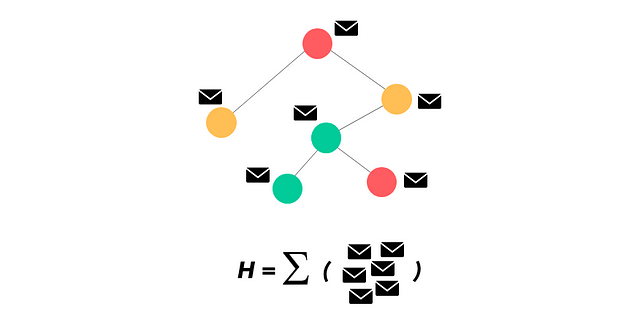
Here’s the final graph with the fully updated node embedding vectors after n repetitions of Message Passing. You can take the representations of all the nodes and sum them together to get H.
📝 Graph Neural Networks, a summary
GNNs are fairly simple to use. In fact, implementing them involved four steps.
- Given a graph, we first convert the nodes to recurrent units and the edges to feed-forward neural networks.
- Then we perform Neighbourhood Aggregation (Message Passing, if that sounds better) for all nodes n number of times.
- Then we sum over the embedding vectors of all nodes to get graph representation H.
- Feel free to pass H into higher layers or use it to represent the graph’s unique properties!
🙇🏻♂️ Why Graph Neural Networks?
Now that we know how Graph Neural Networks work, why would we want to apply/use them?
In the case of social media graphs, GNNs are great at content recommendation. When a user follows other users with a similar taste in political leaning (for example), GNNs can be used for node classification to predict if a certain piece of content on the site can be sent to the news feed of said user.
When suggesting “who to follow”, systems can take into account the industry of the user and provide potential connections–edge classification.
🔩 In a nutshell
Here, we covered the basics of Graph Neural Networks with a bunch of visualisations. Graph DL is really interesting and I urge you to try coding up your own implementation of it. There are tons of graph construction libraries like the Deep Graph Library or PyTorch Geometric.
If you are interested in having a mathematical breakdown of Graph NNs with code snippets explaining the concepts in this article, drop the suggestions in the comment section or shoot me a message (profiles listed below).
There are also great resources to learn about GDL algorithms and different ways to capture lots of sequential and spatial aspects from graph representations. Do explore beyond this article and implement it using your tools of choice.
Until then, I’ll see you in the next one!
Original article by Rishabh Anand
❤️ Love talking tech?
You’re in luck! I love talking about Artificial Intelligence, Data Science, and the progress of science and technology in general. If you want to chat, you can catch me procrastinating on Twitter and LinkedIn.
📞 A call to action…of sorts
Your feedback and constant support mean a lot and encourage me to continue writing high-quality content for both your learning and mine! While you’re waiting for my reply (which is usually very quick 🙌🏻), do check out my other trending articles:
Crash Course in Quantum Computing Using Very Colorful Diagrams
Almost everything you need to know about Quantum Computing explained using very intuitive drawings…
towardsdatascience.com
Training Your Models on Cloud TPUs on Google Colab in 4 Easy Steps
I trained a model on a TPU and now feel like a superhero…
medium.com
A Comprehensive Guide to Genetic Algorithms (and how to code them)
On the Origin of Genetic
Algorithmsmedium.com
CatGAN: cat face generation using GANs
Detailed review of GANs and how to waste your time with them… hackernoon.com
